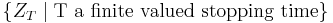Doob–Meyer decomposition theorem

The Doob–Meyer decomposition theorem is a theorem in stochastic calculus stating the conditions under which a submartingale may be decomposed in a unique way as the sum of a martingale and a continuous increasing process. It is named for J. L. Doob and Paul-André Meyer.

1 History
2 Class D Supermartingales
3 The theorem
4 See also
5 Notes
6 References
7 External links

History

In 1953, Doob published the Doob decomposition theorem which gives a unique decomposition for certain discrete time martingales.^[1] He conjectured a continuous time version of the theorem and in two publications in 1962 and 1963 Paul-André Meyer proved such a theorem, which became known as the Doob-Meyer decomposition.^[2]^[3] In honor of Doob, Meyer used the term "class D" to refer to the class of supermartingales for which his unique decomposition theorem applied.^[4]

Class D Supermartingales

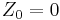A càdlàg supermartingale $Z$ is of Class D if $Z_0=0$ and the collection

$\{Z_T \mid \text{T a finite valued stopping time} \}$

is uniformly integrable.^[5]

The theorem

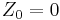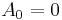Let $Z$ be a cadlag supermartingale of class D with $Z_0 =0$ . Then there exists a unique, increasing, predictable process $A$ with $A_0 =0$ such that 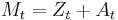$M_t = Z_t %2B A_t$ is a uniformly integrable martingale.^[6]

Notes

^ Doob 1953
^ Meyer 1952
^ Meyer 1963
^ Protter 2005
^ Protter (2005)
^ Protter (2005)

References

Doob, J.L. (1953). Stochastic Processes. Wiley.
Meyer, Paul (1962). "A Decomposition theorem for supermartingales". Illinois Journal of Mathematics 6: 193–205.
Meyer, Paul (1963). "Decomposition of supermartingales: the uniqueness theorem". Illinois Journal of Mathematics 7: 1–17.
Protter, Philip (2005). Stochastic Integration and Differential Equations. Springer-Verlag. pp. 107–113. ISBN 3-540-00313-4.

External links

The Doob–Meyer decomposition theorem with proof, by Jan van Neerven